Home
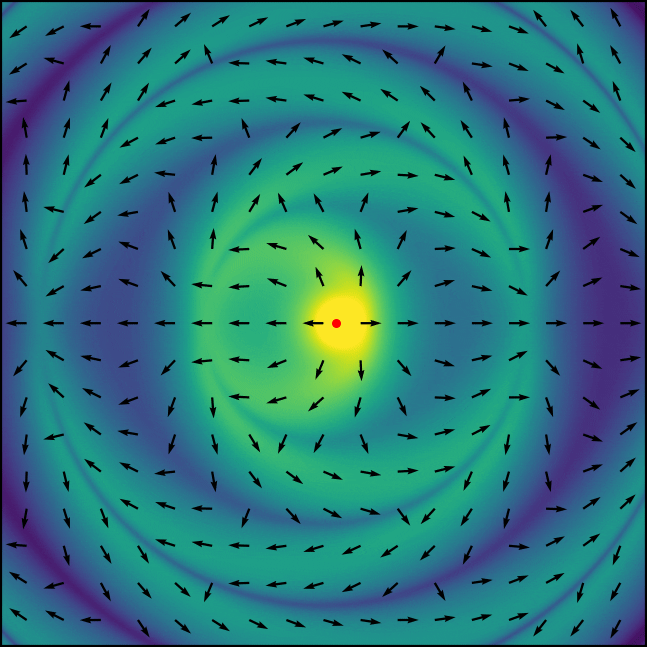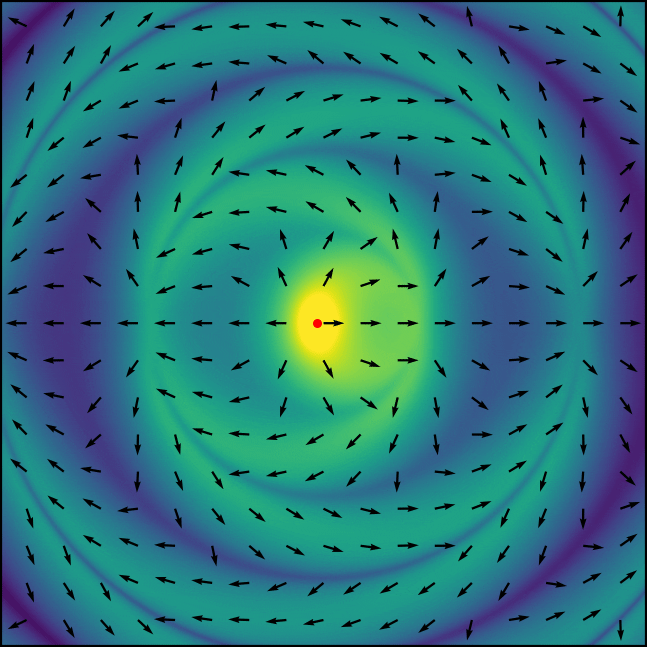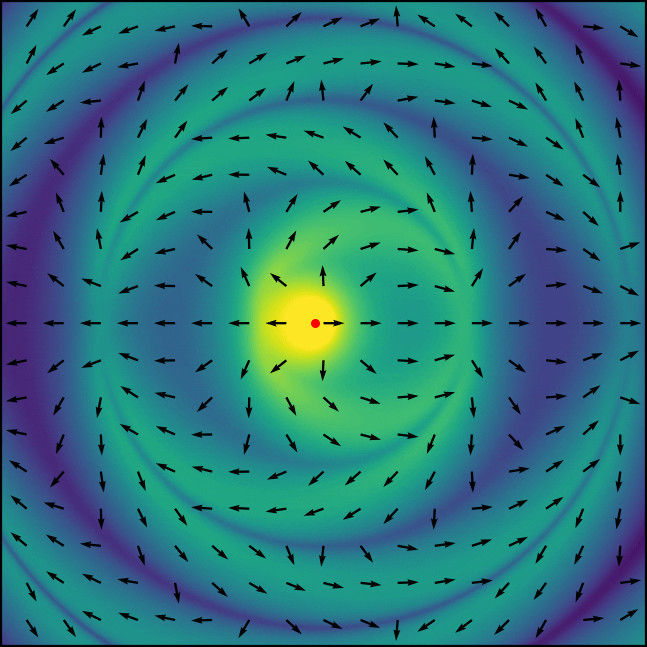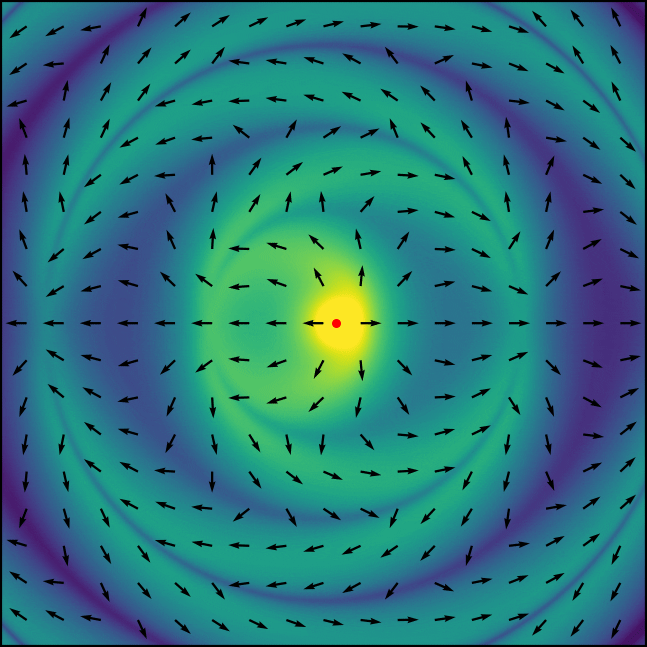
PyCharge is an open-source computational electrodynamics Python simulator that can calculate the electromagnetic fields and potentials generated by moving point charges and can self-consistently simulate dipoles modeled as Lorentz oscillators.
PyCharge was developed to allow both novice and experienced users model a wide range of classical electrodynamics systems using point charges: the package can be used as a pedagogical tool for undergraduate and graduate-level EM theory courses to provide an intuitive understanding of the EM waves generated by moving point charges, and can also be used by researchers in the field of nano-optics to investigate the complex interactions of light in nanoscale environments.
Key Features
- Calculate the relativistically-correct electromagnetic fields and potentials generated by moving point charge sources in a system at specified grid points in space and time. The moving point charges can have custom trajectories.
- Self-consistent simulatations of dipoles modeled as Lorentz oscillators which are driven by the electric field in the system. PyCharge dynamically determines the dipole moment at each time step.
- Expected coupling between dipoles predicted by QED theory is captured in the simulations, and the modified radiative properties of the dipoles (radiative decay rate and frequency shift) can be extracted using the dipole's energy at each time step.
- Moving dipoles can be modelled by specifying the dipole's origin position as a function of time.
- Parallelized version of the dipole simulation method using mpi4py to enable the parallel execution of computationally demanding simulations on high performance computing environments to significantly improve run time.
Our computational physics paper introducing the PyCharge package was published in Computer Physics Communications and is also available on arXiv. The paper includes an extensive review of the rich physics that govern the coupled dipole simulations.
Usage
An overview of the classes and methods implemented in the PyCharge package is shown in the figure below:
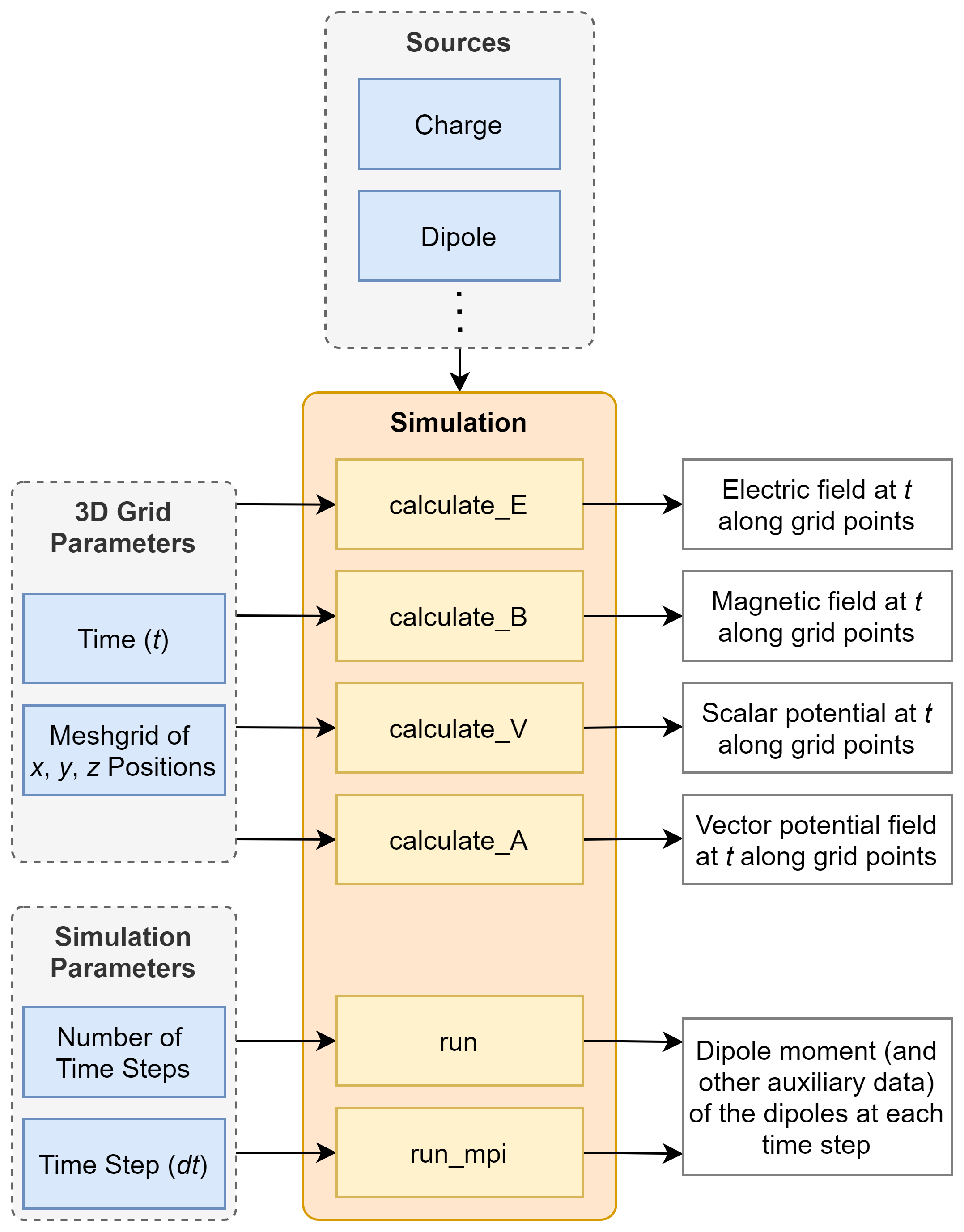
The electromagnetic fields and potentials generated by moving point charges can be calculated using PyCharge with only a few lines of code. The following script calculates the electric field components and scalar potential along a spatial grid in the \(x-y\) plane generated by two stationary charges:
import pycharge as pc
from numpy import linspace, meshgrid
from scipy.constants import e
sources = (pc.StationaryCharge((10e-9, 0, 0), e),
pc.StationaryCharge((-10e-9, 0, 0), -e))
simulation = pc.Simulation(sources)
coord = linspace(-50e-9, 50e-9, 1001)
x, y, z = meshgrid(coord, coord, 0, indexing='ij')
Ex, Ey, Ez = simulation.calculate_E(0, x, y, z)
V = simulation.calculate_V(0, x, y, z)
Two dipoles separated by 80 nm along the \(x\)-axis are simulated over 40,000 timesteps in the script below:
import pycharge as pc
from numpy import pi
timesteps = 40000
dt = 1e-18
omega_0 = 100e12*2*pi
origins = ((0, 0, 0), (80e-9, 0, 0))
init_d = (0, 1e-9, 0)
sources = (pc.Dipole(omega_0, origins[0], init_d),
pc.Dipole(omega_0, origins[1], init_d))
simulation = pc.Simulation(sources)
simulation.run(timesteps, dt, 's_dipoles.dat')
Download and Installation
The PyCharge source repository is hosted on GitHub and installation instructions are given here.
Contributing
We welcome all bug reports and suggestions for future features and enhancements, which can be filed as GitHub issues. To contribute a feature:
- Fork it (https://github.com/MatthewFilipovich/pycharge/fork)
- Create your feature branch (
git checkout -b feature/fooBar) - Commit your changes (
git commit -am 'Add some fooBar') - Push to the branch (
git push origin feature/fooBar) - Submit a Pull Request
Citing PyCharge
If you are using PyCharge for research purposes, we kindly request that you cite the following paper:
M. Filipovich and S. Hughes, PyCharge: An open-source Python package for self-consistent electrodynamics simulations of Lorentz oscillators and moving point charges, Comput. Phys. Commun. 274, 108291 (2022).
License
PyCharge is distributed under the GNU GPLv3. See LICENSE for more information.
Acknowledgements
PyCharge was written as part of a graduate research project at Queen's University (Kingston, Canada) by Matthew Filipovich and supervised by Stephen Hughes.